To effectively navigate the intricacies of thermodynamics problems, a profound apprehension of the fundamental principles presiding over energy conservation is an imperative prerequisite. The First Law of Thermodynamics, a cornerstone of physical science, unequivocally postulates that energy, within the confines of a closed system, remains an inviolable entity; it can neither be spontaneously generated nor utterly annihilated. This foundational tenet underpins all energetic transformations, dictating that the total energy of an isolated thermodynamic ensemble persists in an immutable state, merely transforming between various manifestations.

This seminal law meticulously delineates the intricate interplay between a system’s internal energy, the quantum of heat exchanged with its surroundings, and the work performed upon or by it. It elucidates that any alteration in the intrinsic energetic state of a system is a direct consequence of the net thermal exchange and mechanical exertion traversing its boundaries. Consequently, mastering this relationship is not merely academic; it furnishes the analytical framework necessary for predicting the behavior of systems undergoing thermodynamic processes, from combustion engines to biological systems, highlighting its omnipresence in both natural phenomena and engineered applications.

---

---

A profound grasp of the First Law of Thermodynamics is an indispensable prerequisite for anyone seeking to master the foundational principles of physics and engineering. This pivotal statute, mathematically articulated as ##\Delta U = Q – W##, unequivocally governs the immutable principle of energy conservation within any delineated thermodynamic system.

It posits that energy can neither be created nor destroyed, merely transformed between various manifestations. This exposition aims to illuminate the intricate mechanics of this fundamental law, providing a comprehensive understanding of how the inherent energetic state of a system, its internal energy, is intrinsically linked to the thermal exchange with its environment—represented by heat—and the mechanical or electrical work performed upon or by it.

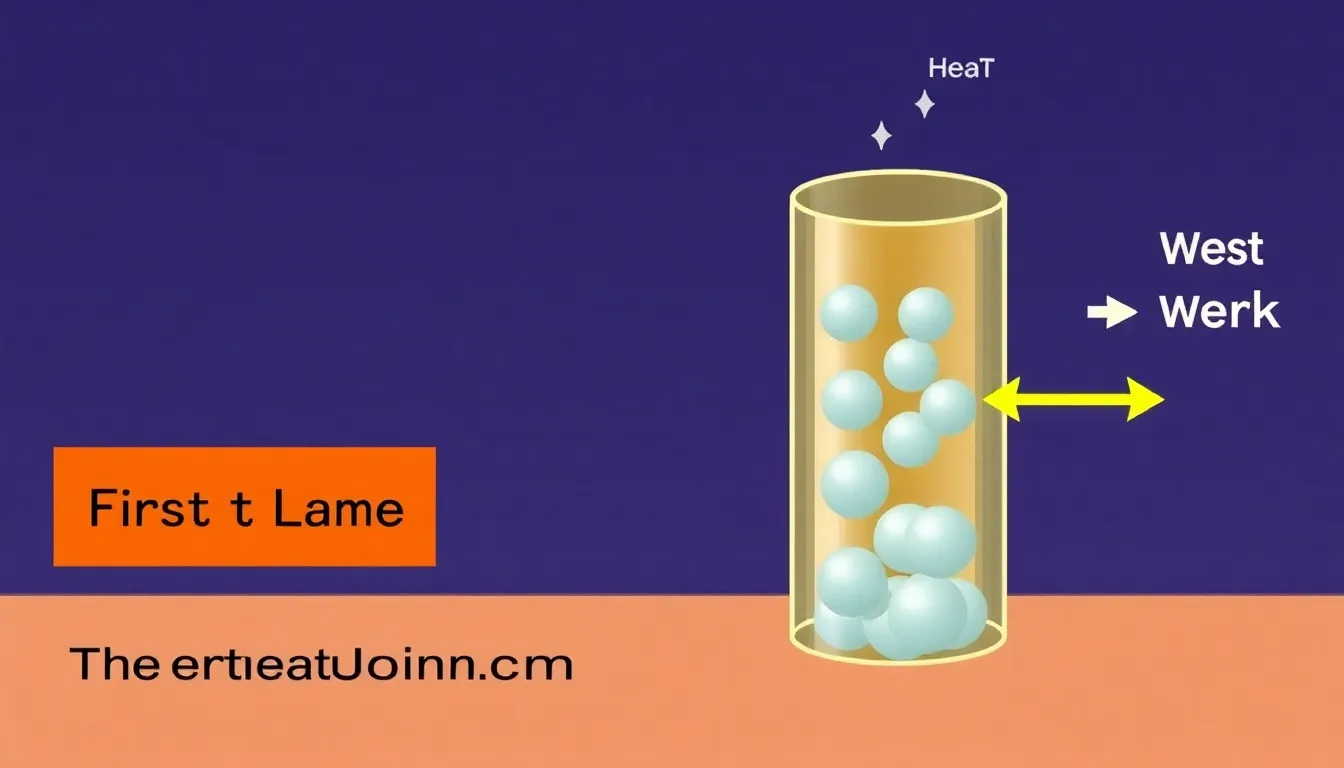
The First Law of Thermodynamics

The First Law of Thermodynamics is one of the most important principles in physics. It asserts that energy can neither be created nor destroyed; it can only change from one form to another. In essence, the total energy of an isolated system remains constant.

This principle applies universally, from the expansion of gases in a cylinder to the operation of heat engines and even to biological processes. The First Law serves as the foundation upon which the rest of thermodynamics is built, guiding how we analyze energy exchanges in physical and chemical systems.

Mathematically, it is expressed as:

### \Delta U = Q – W ###

• ΔU = Change in internal energy of the system
• Q = Heat added to the system
• W = Work done by the system

Defining Internal Energy

The concept of internal energy (ΔU) is central to thermodynamics. It represents the total microscopic energy stored within a system, arising from:

• Kinetic energy: Due to the random motion of molecules (translation, rotation, vibration).
• Potential energy: Due to intermolecular forces and chemical bonds between molecules.

Because internal energy depends solely on the current state of the system (temperature, pressure, and volume), it is classified as a state function. It does not depend on the path taken to reach that state.

Why Internal Energy Matters

A change in internal energy (ΔU) reflects a system’s thermal changes:

• When heat is added and no work is done, the internal energy increases (temperature rises or a phase change occurs).
• When a system does work on its surroundings (expansion of a gas), its internal energy decreases if no additional heat is supplied.
• In many natural processes, both heat transfer and work occur, and the balance determines how ΔU changes.

Measurement Challenges

Measuring absolute internal energy is practically impossible because it encompasses all microscopic interactions. However, changes in internal energy (ΔU) can be computed indirectly using:

### \Delta U = Q – W ###

This relationship allows scientists and engineers to analyze energy transformations in real-world systems without needing to measure molecular energies directly.

Summary Table

Concept	Description
First Law	Energy is conserved; ΔU = Q – W
Internal Energy	Total microscopic energy (kinetic + potential) of molecules
State Function	Depends only on system’s current state, not path
Measurement	ΔU determined indirectly via heat and work exchange

Illustrative Problem

Problem: A system absorbs 600 J of heat and performs 250 J of work. What is the change in internal energy?

Solution: ### \Delta U = Q – W = 600 – 250 = 350 \,\text{J} ###

Answer: The internal energy of the system increases by 350 J.

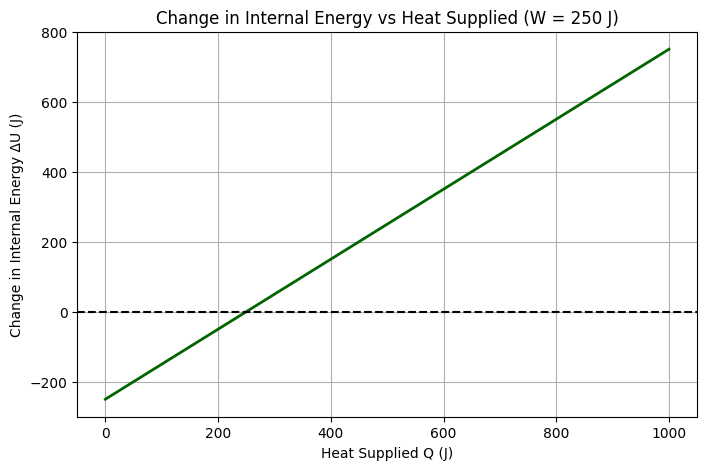
Understanding Heat (Q)

In thermodynamics, heat (Q) refers to the transfer of energy between a system and its surroundings because of a temperature difference. It is not a substance contained within matter, but rather a form of energy in transit.

Sign Convention for Heat

• Q > 0: Heat is added to the system (energy flows into the system, internal energy increases).
• Q < 0: Heat is removed from the system (energy leaves the system, internal energy decreases).

This convention is essential for applying the First Law of Thermodynamics:

### \Delta U = Q – W ###

Modes of Heat Transfer

Heat can be transferred in three primary ways:

• Conduction: Direct transfer through molecular collisions within solids (e.g., a metal rod heated at one end).
• Convection: Transfer via bulk movement of fluids (e.g., boiling water, atmospheric circulation).
• Radiation: Transfer through electromagnetic waves, requiring no medium (e.g., sunlight reaching Earth).

Why Heat Transfer Matters

The amount and direction of heat transfer directly determine whether a system’s internal energy rises or falls. This makes heat analysis central to understanding processes such as:

• Heating and cooling of gases
• Phase changes (melting, boiling, condensation)
• Operation of engines, refrigerators, and heat pumps

Summary Table of Heat Transfer

Condition	Q Value	Effect on System	Example
Heat Added	Q > 0	Internal energy increases	Heating water on a stove
Heat Removed	Q < 0	Internal energy decreases	Ice melting in a warm room

Example Problem

Problem: A system absorbs 400 J of heat. If it does 150 J of work, what is the change in internal energy?

Solution:

### \Delta U = Q – W = 400 – 150 = 250 \,\text{J} ###

Answer: The internal energy increases by 250 J.

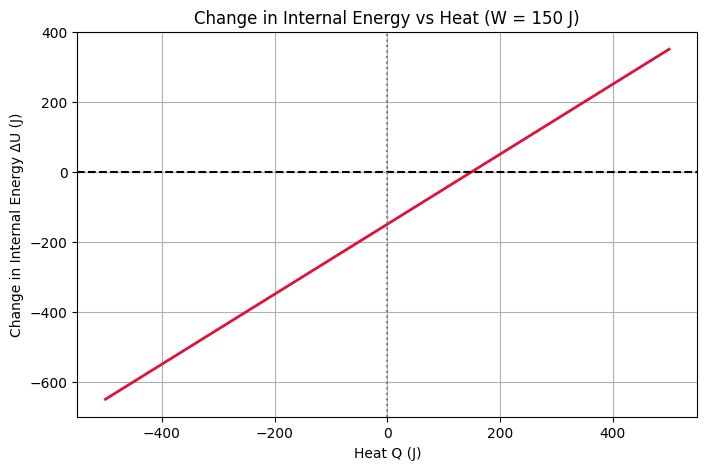
This graph would show how the system’s internal energy increases when heat is added (Q > 0) and decreases when heat is removed (Q < 0), always accounting for the work performed.

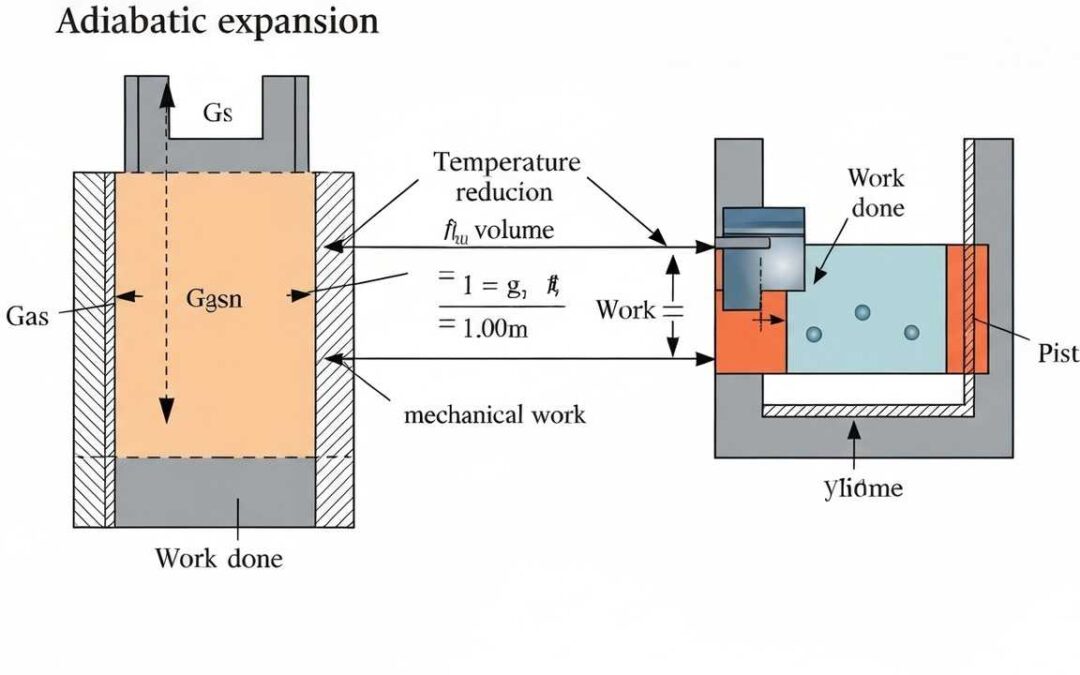
Defining Work (W)

In physics, work (W) is the energy transferred when a force acts upon an object and causes displacement. In thermodynamics, this concept extends to processes like the expansion or compression of gases. Work is a crucial mechanism through which a system can exchange energy with its surroundings, alongside heat transfer.

Work Sign Convention

• W > 0: Work done by the system on the surroundings (system loses energy).
• W < 0: Work done on the system by the surroundings (system gains energy).

This sign convention ensures the correct application of the First Law of Thermodynamics:

### \Delta U = Q – W ###

Here, the work term reduces internal energy if the system performs work, and increases it if work is done on the system.

Types of Work in Thermodynamics

Although pressure–volume (PV) work is the most common, thermodynamic work can take various forms:

• PV Work: Expansion or compression of gases.
• Electrical Work: Movement of charges in electric fields.
• Magnetic Work: Interaction with magnetic fields.
• Gravitational Work: Changes in potential energy due to position in a gravitational field.

Mathematical Expression of PV Work

For infinitesimal expansion or compression of a gas:

### \delta W = P \, dV ###

where P is pressure and dV is the change in volume. Integrating gives:

### W = \int_{V_i}^{V_f} P \, dV ###

This formula highlights that work depends not only on initial and final states, but also on the path of the process.

Example Problem

Problem: A gas expands isobarically (at constant pressure) from 2 m³ to 5 m³ at a pressure of 100 kPa. Calculate the work done.

Solution:

### W = P \Delta V = (100 \times 10^3)(5 – 2) = 300,000 \,\text{J} ###

Answer: The gas does 300 kJ of work on the surroundings.

Summary of Work in Thermodynamics

Condition	Sign of W	Effect on System	Example
Work by system	W > 0	Internal energy decreases	Gas expansion pushing a piston
Work on system	W < 0	Internal energy increases	Piston compressing a gas

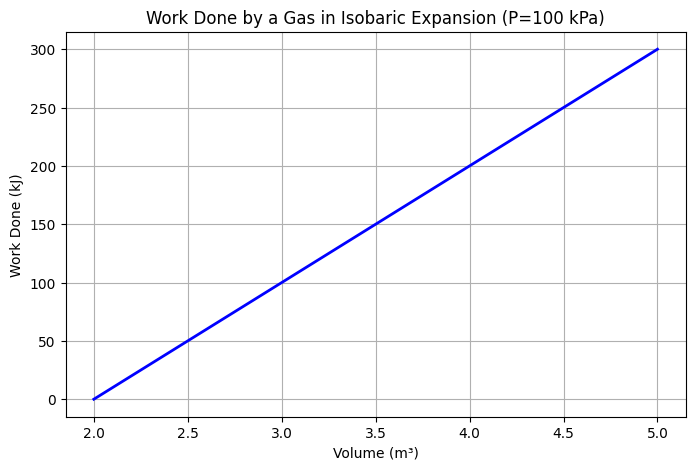
The graph illustrates that as the gas expands, the work done on the surroundings increases linearly with the change in volume under constant pressure.

Solving a First Law Thermodynamics Problem

We analyze a closed system (a gas in a cylinder with a movable piston) that absorbs 500 J of heat and performs 200 J of work on its surroundings. The First Law of Thermodynamics states the energy balance between heat, work, and internal energy as:

###\Delta U = Q – W###

Here, ##\Delta U## is the change in internal energy of the system, ##Q## is the heat added to the system, and ##W## is the work done by the system. With this sign convention: heat in is positive, work by the system is positive. Our goal is to compute ##\Delta U## and interpret the result physically and numerically, then generalize with additional examples, tables, and a simple visual plot.

Givens, Units, and Setup

• Heat added: ##Q = +500\ \text{J}##
• Work by the system: ##W = +200\ \text{J}##
• Unknown: ##\Delta U##
• Units: SI Joules; keep all terms in Joules to avoid conversion errors (##1\ \text{kJ} = 1000\ \text{J}##).

Quantity	Symbol	Sign Meaning	Value	Unit
Heat (to system)	##Q##	Positive when absorbed	+500	J
Work (by system)	##W##	Positive when done by system	+200	J
Change in internal energy	##\Delta U##	Positive when internal energy rises	?	J

Step-by-Step Solution

1. Write the First Law. ###\Delta U = Q – W###
2. Substitute numbers. ###\Delta U = 500\ \text{J} – 200\ \text{J}###
3. Compute. ###\Delta U = 300\ \text{J}###

Result: The gas’s internal energy increases by ##300\ \text{J}##. The system kept part of the incoming heat and spent the rest doing useful work: the “stored” part manifests as higher microscopic kinetic/potential energy of the molecules.

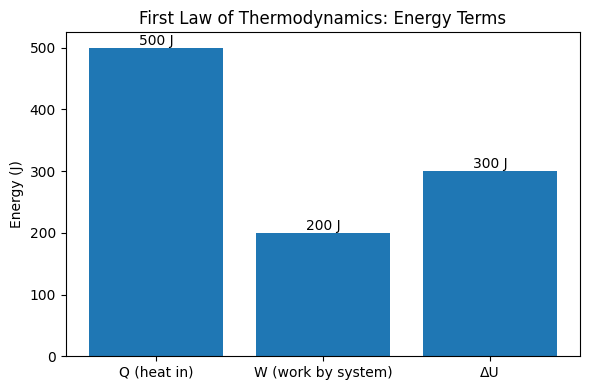
Interpretation & Quick Checks

• Energy bookkeeping: Incoming heat (500 J) is partitioned into work out (200 J) and internal storage (300 J). Energy is conserved.
• Sign sanity check: Heat absorbed tends to increase ##\Delta U##; work done by the system tends to decrease ##\Delta U##—exactly what ###\Delta U = Q – W### encodes.
• Units: All terms carry Joules; mismatched units are a common source of mistakes.

Sign Conventions (Know Which One You Use)

Different textbooks/courses may flip the sign on work. The following table contrasts two common conventions. The numbers and physics agree once you are consistent.

Convention	Heat	Work	First-Law Form	Example Mapping
Used in this solution	##Q>0## when heat enters system	##W>0## when work is done by system	###\Delta U = Q – W###	Absorb 500 J, do 200 J by system → ##Q=+500, W=+200##
Alternative (work-on-system positive)	##Q>0## when heat enters system	##W_\text{on}>0## when work is done on the system	###\Delta U = Q + W_\text{on}###	Same situation → ##W_\text{on}=-200##, so ###\Delta U=500+(-200)=300###

Additional Worked Examples

Problem 1: Heat Released; Work Done On the System

A gas releases 250 J of heat to the surroundings and 100 J of work is done on the gas. Using the “work by system is positive” convention: ##Q = -250\ \text{J}## (released), ##W = -100\ \text{J}## (since work is on the system).

Solution: ###\Delta U = Q – W = (-250) – (-100) = -150\ \text{J}###. The internal energy decreases by 150 J.

Problem 2: Cyclic Process

Over one complete cycle a system absorbs ##Q=1200\ \text{J}## and does ##W=1200\ \text{J}## of work. Find ##\Delta U## for the cycle.

Solution: ###\Delta U = Q – W = 1200 – 1200 = 0###. In a cycle the internal energy returns to its initial value.

Problem 3: Find the Heat Transfer

A system’s internal energy decreases by ##50\ \text{J}## while it does ##350\ \text{J}## of work on the surroundings. What is ##Q##?

Solution: From ###\Delta U = Q – W###, rearrange to ###Q = \Delta U + W###. Hence ###Q = (-50) + 350 = 300\ \text{J}###. The system must have absorbed 300 J of heat even though its internal energy fell (because it did substantial work).

Problem 4: Constant-Volume Heating

At constant volume, boundary work is zero: ##W=0##. Suppose the system absorbs ##Q=2.4\ \text{kJ}## at constant volume. Compute ##\Delta U## (in kJ).

Solution: ###\Delta U = Q – W = 2.4 – 0 = 2.4\ \text{kJ}###. At constant volume, heat directly raises internal energy: ###\Delta U = Q###.

Quick Tips & Pitfalls

• Set the sign convention first. Are you using “work by system is positive” (this lesson) or “work on system is positive”? Consistency prevents errors.
• Mind the units. Keep heat, work, and internal energy in the same units (J or kJ). Convert early.
• Closed vs. open systems. For open systems (steady-flow devices), the energy balance includes flow work and enthalpy; here we strictly considered a closed system.

Valuable insights

Applying the First Law with the given data and sign convention yields ###\Delta U = 300\ \text{J}###. The gas stores part of the absorbed heat as internal energy and expends the rest as work. The same reasoning scales to a wide range of thermodynamic processes once signs, units, and system boundaries are set with care.

Numerical Problems

Problem 1

A system absorbs 100 J of heat and does no work. What is the change in internal energy?

Problem 2

A system releases 50 J of heat and has 20 J of work done on it. What is the change in internal energy?

Problem 3

A system absorbs 200 J of heat and does 100 J of work. What is the change in internal energy?

Problem 4

A system releases 75 J of heat and does 75 J of work. What is the change in internal energy? Answer: ##\Delta U = 0 J##

Problem 5

A system absorbs 150 J of heat, and 50 J of work is done on the system. What is the change in internal energy?

First Law Problems: Detailed Solutions & Visualization

We use the closed-system convention ###\Delta U = Q – W###, where ##Q## is heat added to the system (positive when absorbed) and ##W## is work done by the system on the surroundings (positive when the system does work). If work is done on the system, then ##W<0## for this convention.

Problem 1

Prompt. A system absorbs 100 J of heat and does no work. What is the change in internal energy?

Given. ##Q = +100\ \text{J}##, ##W = 0##.

Compute. ###\Delta U = Q – W = 100 – 0 = 100\ \text{J}###.

Answer. ##\Delta U = +100\ \text{J}## (internal energy increases).

Problem 2

Prompt. A system releases 50 J of heat and has 20 J of work done on it. What is the change in internal energy?

Given. Releases heat → ##Q = -50\ \text{J}##. Work done on the system → ##W = -20\ \text{J}## (negative because it is not work by the system).

Compute. ###\Delta U = Q – W = (-50) – (-20) = -30\ \text{J}###.

Answer. ##\Delta U = -30\ \text{J}## (internal energy decreases).

Problem 3

Prompt. A system absorbs 200 J of heat and does 100 J of work. What is the change in internal energy?

Given. ##Q = +200\ \text{J}##, ##W = +100\ \text{J}##.

Compute. ###\Delta U = 200 – 100 = 100\ \text{J}###.

Answer. ##\Delta U = +100\ \text{J}##.

Problem 4

Prompt. A system releases 75 J of heat and does 75 J of work. What is the change in internal energy?

Given. ##Q = -75\ \text{J}##, ##W = +75\ \text{J}##.

Compute. ###\Delta U = -75 – 75 = -150\ \text{J}###.

Corrected Answer. ##\Delta U = -150\ \text{J}##. (The previously stated “##\Delta U = 0\ \text{J}##” is incorrect under this sign convention.)

Problem 5

Prompt. A system absorbs 150 J of heat, and 50 J of work is done on the system. What is the change in internal energy?

Given. ##Q = +150\ \text{J}##, work on system → ##W = -50\ \text{J}##.

Compute. ###\Delta U = 150 – (-50) = 200\ \text{J}###.

Answer. ##\Delta U = +200\ \text{J}##.

Summary Table

Problem	Heat ##Q## (J)	Work ##W## (J)	Computation	##\Delta U## (J)	Interpretation
P1	+100	0	###100 – 0###	###+100###	Internal energy increases
P2	-50	-20	###-50 – (-20)###	###-30###	Internal energy decreases
P3	+200	+100	###200 – 100###	###+100###	Internal energy increases
P4	-75	+75	###-75 – 75###	###-150###	Internal energy decreases
P5	+150	-50	###150 – (-50)###	###+200###	Internal energy increases

Code to Recreate the Plot

This Matplotlib-only snippet (single plot, default colors) reproduces the figure.

Key Takeaways

• Use the sign convention consistently: ###\Delta U = Q – W### with ##W>0## for work by the system.
• “Work done on the system” implies ##W<0## under this convention.
• Positive ##\Delta U## means energy stored internally increased; negative means it decreased.

---

---