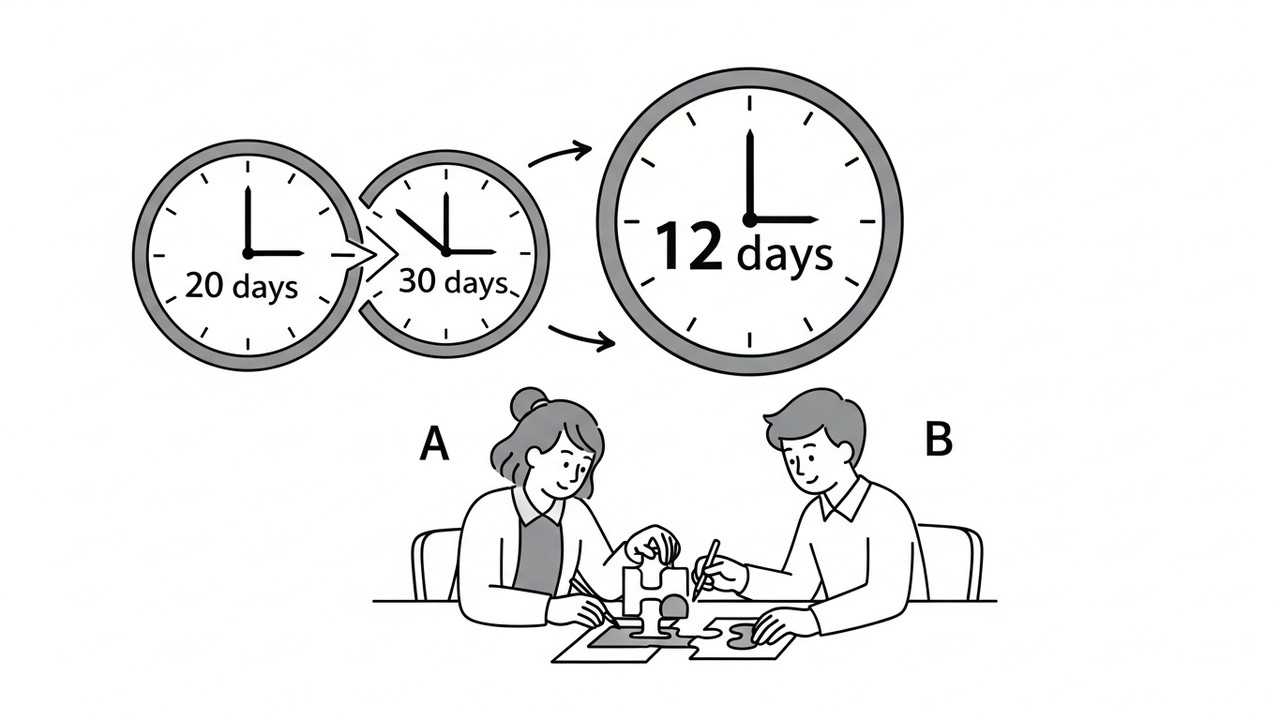
General aptitude often involves solving work rate problems where collaboration is key. In this case, A completes a task in 20 days and B in 30 days, and we’ll explore how quickly they can finish together, applying basic arithmetic and logical reasoning to find the solution efficiently.
Table of Contents
Read More
Collaborative work problems are a staple in aptitude tests, assessing your ability to calculate combined efforts efficiently. Understanding how individuals A and B contribute can streamline solving such puzzles.
Decoding Individual Work Rates
Each person’s work rate is fundamental to solving joint tasks. A’s rate is 1/20 of the work per day, while B’s is 1/30 per day.
Calculating A’s Daily Output
A completes the entire task in 20 days, so their daily contribution is 1/20. This means if A works alone, they finish 5% of the work each day.
This rate is crucial for summing efforts when multiple people are involved, as it sets the baseline for collaboration calculations.
Assessing B’s Efficiency
B takes 30 days to finish the work alone, resulting in a daily rate of 1/30. This slower pace highlights differences in individual capabilities.
Recognizing such variances helps in real-world scenarios where team members have diverse skills and speeds.
Combining Efforts for Faster Completion
When A and B work together, their rates add up, leading to a quicker finish. The combined daily rate is the sum of their individual rates.
Summing the Work Rates
Add A’s rate of 1/20 and B’s rate of 1/30. To do this, find a common denominator, which is 60, so it becomes 3/60 + 2/60 = 5/60 or 1/12 per day.
This simplified rate indicates that together, they complete 1/12 of the work daily, making the math straightforward for further steps.
Determining Total Time Required
With a combined rate of 1/12 per day, the time to finish the entire work is the reciprocal, which is 12 days. This is derived from 1 divided by (1/12).
Such calculations are essential in aptitude tests to evaluate problem-solving skills under time constraints.
Key Takeaways
Mastering work rate problems enhances your general aptitude for exams. Always sum individual rates and take the reciprocal for the joint completion time. Practice with varied scenarios to build confidence.
| Person | Time to Complete Alone (days) | Daily Work Rate |
|---|---|---|
| A | 20 | 1/20 |
| B | 30 | 1/30 |
| A and B Together | 12 | 1/12 |
We also Published
RESOURCES
- General Aptitude Test – Aptitude-test.com
- General Aptitude Contract : r/AirForceRecruits
- The role of mind-wandering in measurements of general aptitude
- General Aptitude : r/AirForceRecruits
- Fairness in Employment Testing: Validity Generalization, Minority …
- ED164579 – Manual for the USES General Aptitude Test … – ERIC
- GA General Aptitude
- Aptitude Questions and Answers – GeeksforGeeks
- Does anyone have General Aptitude in the Air Force?
- ASVAB – U.S. Air Force







0 Comments