General aptitude often hinges on mastering averages, a cornerstone of arithmetic reasoning. In this exploration, we unravel a classic problem where removing one number alters the average, showcasing essential skills for test success. Dive in to enhance your quantitative prowess with practical insights and step-by-step guidance.
Table of Contents
Read More
General aptitude tests frequently challenge candidates with problems involving averages, requiring a blend of arithmetic skill and logical reasoning. This classic problem, where the average shifts upon removal of a number, serves as an excellent exercise to sharpen your quantitative abilities.
Understanding the Core Concept of Averages
Averages, or means, are fundamental in statistics and everyday calculations, representing the central value of a dataset. They are pivotal in aptitude exams for assessing numerical proficiency.
Definition and Formula
The average of a set of numbers is calculated by summing all values and dividing by the count. For instance, with five numbers, the sum is five times the average, a key insight for solving such problems.
This formula, ##\text{Average} = \frac{\text{Sum}}{\text{Count}}##, allows manipulation when values change, making it versatile for various scenarios in tests.
Importance in Aptitude Testing
Averages are commonly tested because they evaluate basic arithmetic and problem-solving skills under time constraints. Many competitive exams include them to filter candidates efficiently.
Mastering average problems can boost scores significantly, as they often appear in sections dedicated to quantitative aptitude and data interpretation.
Solving the Specific Problem Step by Step
Let’s dive into the given problem: with an initial average of 28 for five numbers, removal of one number raises the average to 30 for the remaining four.
Step 1: Calculate the Total Sum Initially
Using the average formula, the sum of the five numbers is ##5 \times 28 = 140##. This total is crucial for finding the removed number later in the solution.
Remember, this sum remains constant until numbers are altered, providing a stable reference point for calculations.
Step 2: Find the Sum After Removal
After removing one number, the average of the remaining four is 30, so their sum is ##4 \times 30 = 120##. This step isolates the effect of the removal on the total.
The difference between the original sum and this new sum directly gives the value of the removed number, as no other changes occur.
Step 3: Determine the Removed Number
Subtract the sum after removal from the original sum: ##140 – 120 = 20##. Thus, the removed number is 20, a straightforward arithmetic result.
This method can be generalized to similar problems with different counts and averages, enhancing problem-solving versatility.
Step 4: Verify the Solution
To ensure accuracy, check if removing 20 from the set of five numbers with sum 140 leaves a sum of 120 for four numbers, yielding an average of 30, which confirms the answer.
Verification is a best practice in aptitude tests to avoid errors and build confidence in your solutions.
Key Takeaways
This problem illustrates the power of understanding averages in aptitude contexts. By mastering the formula and steps, you can tackle a wide range of quantitative challenges efficiently.
Always remember to calculate sums before and after changes, and use differences to find unknown values, a strategy applicable beyond this specific scenario.
| Step | Calculation | Result |
|---|---|---|
| Initial Sum | 5 × 28 | 140 |
| Sum After Removal | 4 × 30 | 120 |
| Removed Number | 140 – 120 | 20 |
We also Published
RESOURCES
- General Aptitude Test – Aptitude-test.com
- General Aptitude Contract : r/AirForceRecruits
- The role of mind-wandering in measurements of general aptitude
- General Aptitude : r/AirForceRecruits
- Fairness in Employment Testing: Validity Generalization, Minority …
- ED164579 – Manual for the USES General Aptitude Test … – ERIC
- GA General Aptitude
- Aptitude Questions and Answers – GeeksforGeeks
- Does anyone have General Aptitude in the Air Force?
- ASVAB – U.S. Air Force
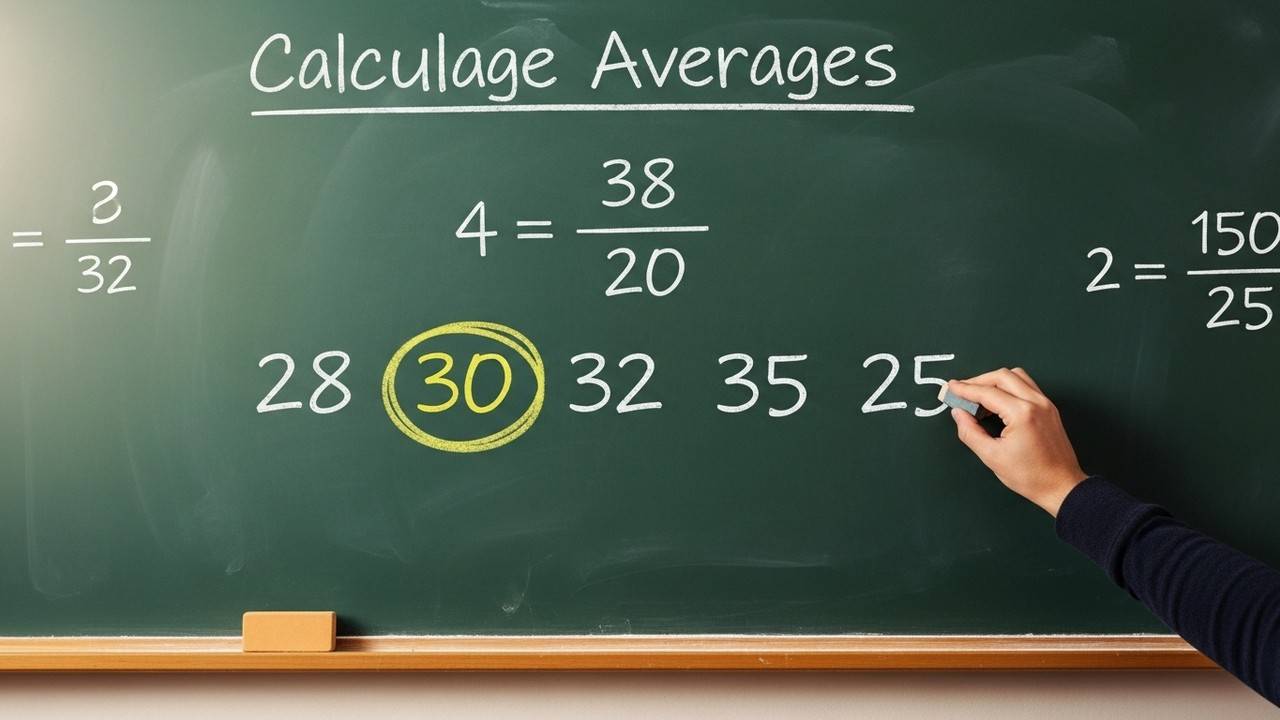






0 Comments